Este artigo precisa ser limpo para cumprir o guia de estilo. [discutir] Por favor, ajude a melhorar esta página. A página de discussão pode conter sugestões.
Este artigo precisa ser limpo para cumprir o guia de estilo. [discutir] Por favor, ajude a melhorar esta página. A página de discussão pode conter sugestões.
 Este artigo usa esquemas MCRedstoneSim.
Eles devem ser convertidos para usar {{schematic}} se possível.
Este artigo usa esquemas MCRedstoneSim.
Eles devem ser convertidos para usar {{schematic}} se possível.
Conteúdo
- 1 somadores
- 1.1 versão 1
- 1.2 In-Line Adder
- 1.3 versão 2
- 1.4 versão 3
- 1.5 Adição Rápida
- 1.6 Adicionadores de Pistão
- 1.7 Adicionador de 4 bits
- 1.8 Adicionador Alternativo de 4 bits
- 2 subtração
- 3 unidades lógicas
Adders
versão 1

Captura de tela do somador completo no jogo
Adicionador completo 1
Veja em: Tutoriais / Logic gates / Full Adder 1 [editar] Full AdderUm somador completo pega duas entradas A e B e uma entrada Carry e produz as saídas Soma e Carry. Ele se baseia em duas portas XOR, duas portas AND e uma porta OR. Pensando bem, essas portas podem ser comprimidas (já que as portas AND e XOR já existem no jogo, e uma porta OR pode ser simplesmente um fio de redstone).
A e B são as entradas de bit e C 'é o carry in. Ele produz uma soma em S e um carry out em C. Quando os módulos somadores completos são agrupados, C' e C serão conectados, o que permite que o carry se propague para o próximo módulo.
Esquema Completo de Somador
 Meio somador
Meio somador
O meio somador é quase idêntico ao somador completo, exceto que a segunda porta XOR é removida e a saída da primeira porta XOR se torna S. Não há carry in (C '), mas o circuito carry out (C) ainda está ligado topo da primeira porta XOR e fornece um transporte para o primeiro somador completo. Algumas ALUs não usarão meio somador para o primeiro bit, para suportar INCREMENT (permitir um carry in no primeiro bit).
In-Line Adder
Full Adder

Captura de tela do jogo de 2 Full Adder
Este somador completo é semelhante ao anterior, exceto pelo fato de que é dois largos e as entradas estão alinhadas verticalmente. Este design é ótimo para minimizar o espaço horizontal e pode ser construído em linha com dois barramentos redstone, eliminando o espaço necessário para expandir um barramento para alcançar as entradas de um somador completo mais amplo.
Esquema do Full Adder
| Vídeo tutorial (ver no YouTube) |
|---|
versão 2
Full AdderPortões: XNOR (2), IMPLIES, NOT, OR, AND
Tamanho: 6 × 12 × 5 (incluindo espaços de E / S)
Este somador pegará 2 bits e um bit transportado (na verdade C, em vez de C, um valor mantido no redstone no canto esquerdo inferior da camada 1) e os adicionará todos juntos, produzindo um bit de soma (S) e um bit de transporte (na verdade, C em vez de C).
Ao usar os portões acima; preste atenção às entradas e saídas. Você pode estar se perguntando por que há tantos sinais invertidos sendo usados em vez do sinal regular.
Os somadores mostrados aqui usam portas XNOR em vez de portas XOR porque são mais compactos e, como resultado, implica que portas devem ser usadas em vez de portas AND, que também são mais compactas.
Portanto, para o somador mais compacto, sinais inversos devem ser usados. Esses somadores são muito complexos para serem facilmente decifrados com 2 camadas por quadrado, portanto, cada camada foi desenhada separadamente para facilitar o processo de construção.
Esquema do Full Adder Meio somador
Meio somador
Portões: XNOR, IMPLIES
Tamanho: 5 × 4 × 4
Este somador pegará 2 bits e os adicionará. O bit resultante será a saída de S (soma). Se ambos os bits forem 1, haverá um transporte e C se tornará 1 (C se tornará 0). Este meio somador pode ser modificado para criar uma saída C não invertida, mas esta configuração é usada para que possa ser implementada como o início de uma cadeia de somadores completos.
Extensão: para aqueles que não conhecem o redstone avançado como eu, é mais fácil entendê-lo assim: digamos que a saída B (C) tem uma porta NOT que inverte o sinal e leva a uma porta de ferro ou porta de pistão, etc. A saída A (S) é conectado a pistões pegajosos que controlam o chão. Digamos, para fins de argumentação, que haja 1 × 1 × 1 bloco NÃO afetado pelos pistões pegajosos, este é o bloco de segurança. Quando você ativa a entrada A, a porta abre e o chão desce, se você estiver no bloco de segurança, não cairá. A entrada B controlará apenas o piso, mas se a entrada A estiver na entrada B controlará os dois. Quando ambos estão ativados, a entrada A afetará apenas o piso. Isso significa que se você estiver fora do servidor e não quiser que ninguém entre, deixe A e B ligados, quando desativarem A, o piso cairá, mas a porta permanecerá fechada, portanto, se souberem do segredo, ainda não poderão entrar.
Esquema do Meio Somador

versão 3
Full AdderTamanho: 5 × 6 × 3
A entrada e a saída do transporte são alinhadas para conectar facilmente muitos desses módulos em série.
Esquema do Full Adder
Adição rápida
Ao construir circuitos digitais avançados, como computadores e multiplicadores, os somadores usados devem ser o mais rápidos possível para garantir a velocidade máxima de execução. Os somadores simples têm um problema fundamental de velocidade que vários projetos de somadores tentam corrigir para acelerar. O problema é o atraso de propagação do carry: atraso causado pela maneira como os somadores pegam os carregamentos. Podemos ver isso quando fazemos o problema 1111 + 0001:
1111 0001 ---- 1110
Esta é a primeira etapa do processo de adição, fazendo o XOR das duas entradas. Como havia dois 1s no bit menos significativo, a porta AND é ativada e carregada para o próximo bit:
1 1111 0001 ---- 1100
Mas aqui está o problema: agora você precisa pegar emprestado um carry novamente, porque, no lugar dos dois, há dois uns. Isso é feito por AND da saída do primeiro meio-somador com o transporte do bit anterior e este é um grande problema. Porque, para a próxima parte, você AND o emprestado carrega novamente e novamente. Cada porta AND leva 2 ticks, portanto, para calcular todos os carregamentos que precisam ser somados na etapa final, leva 2 ticks vezes 4 bits, ou 8 ticks.
Imagine que você vê o problema 999 + 1. Você não fica pensando "9 + 1 é 10, carregue 1, então 9 + 1 é 10, carregue 1, então 9 + 1 é 10, então 1000." É a mesma situação em um circuito avançado.
Engenheiros elétricos reais e redstoners criativos desenvolveram circuitos que calculam carregamentos de somadores mais rápido do que este método sequencial.
Incidentalmente, somadores que calculam carrega um de cada vez desta maneira são chamados Somadores de Ripple Carry.
Adicionadores de pistão
Uma das maneiras mais simples e clássicas de resolver o problema do carry por ondulação é usar portas AND instantâneas que usam pistões. Esses somadores são simples e rápidos, mas são inconstantes porque usam pistões. Quando os blocos são derrubados acidentalmente, todo o circuito é interrompido. Os pistões também apresentam problemas de tempo que podem ser terrivelmente inconvenientes ao construir um circuito avançado que depende muito do tempo.

Sempre que um transporte é criado, ele é enviado através do fio com a alavanca nele e, em vez de passar por uma porta AND, o pistão se retrai e o transporte pode passar para o próximo bit, o que não adiciona nenhum retardo de propagação de transporte ( até que a intensidade do sinal acabe).
Este vídeo mostra uma implementação direta da lógica. O design é grande e espalhado, então é fácil ver cada parte individual do somador e a lógica de transporte.
4-bit Adder
Gates: XNOR (7), IMPLIES (4), NOT (4), OR (3), AND (3)
Tamanho: 23X12X5
Observação! O dígito menos significativo (dígito "uns") está à esquerda do diagrama para que a progressão de meio somador para somador completo possa ser vista mais claramente. Inverta o diagrama se desejar uma entrada convencional da esquerda para a direita.
Este somador pegará números de 2, 4 bits (A e B) e os somará, produzindo um bit de soma (S) para cada bit adicionado e um transporte (C) para a soma total. Os bits de soma estão na mesma ordem dos bits de entrada, o que no diagrama significa que a saída S mais à esquerda é o dígito menos significativo da resposta. Este é apenas um exemplo de uma string de somadores; somadores podem ser encadeados dessa maneira para adicionar números maiores também.
Esquema de somador de 4 bits
Adicionador de 4 bits alternativo
A mesma função, mas um design diferente com 4 somadores completos em vez de 1 meio somador e 3 somadores completos
NOTA: os interruptores são as entradas A e B (entrada do interruptor superior C)
Esquema de somador alternativo de 4 bits
Subtraindo
Subtrair e adicionar são a mesma coisa quando reduzido à ideia de que, por exemplo, 3-2 = 3 + (-2) = 1. Uma vez que já temos a estrutura para adicionar bits, é bastante simples subtrair por apenas adicionando a parte negativa. O problema está na representação de números negativos.
Todos nós estamos familiarizados com o conceito de escola primária de "tomar emprestado" na subtração da próxima coluna como esta:
5623 --128 -----
Não somos capazes de tirar 8 de três, então "pegamos emprestado" um 1 da próxima casa decimal para nos permitir subtrair 8 de 13, resultando em 5
1 5623 --128 ----- 5
Os computadores não são capazes de fazer suposições, portanto, quando um computador precisa encontrar um negativo, ele não coloca (e não pode) colocar um sinal negativo na frente da entrada. Ele apenas subtrai de zero o "empréstimo" da próxima coluna assim:
000000 - 3 ------- -999997
É o mesmo em binário. Vamos, por exemplo, usar um número binário de 4 bits para o exemplo:
1 11 111 1111 0000 0000 0000 0000 0011 -0011 -0011 -0011 -1 ----- ----- ----- ----- ----- 01 --101 --1101 -XNUMX
Poderíamos repetir isso para sempre, mas seria inútil. Isso é sobre o que um registro de 4 bits faz: ele trunca após 4 bits de dados. Então, depois de truncarmos o número (o que eu gentilmente fiz para você no exemplo, caso contrário, o número teria um número infinito de 1s à esquerda). Graças a esse pequeno privilégio, podemos fazer o que quisermos com os 0s após os quatro, incluindo (o que será fantasticamente útil mais tarde) adicionar um único 1 na frente deles.
10000 -0011 ----- 1101 <- NOTA: Este número é positivo! Sucesso!
Lembra como dissemos que nosso redstone não tinha uma maneira especial de designar um negativo de um positivo? Acabamos de criar um caminho. Se o bit mais significativo (primeiro) de um número for 1, significa que é um número negativo. Esta fantástica vantagem dos números binários é um teorema chamado "Complemento de Dois".
Formalmente, o Complemento de Dois é definido como:
O negativo de um número b com comprimento de bit n é igual a 2n + 1 - b
Essencialmente, o que isso quer dizer é que −b é apenas a inversão de b (troque 1's por 0's e 0's por 1's) mais 1.
O que fizemos foi transformar o primeiro bit em um "sinal negativo" se estiver ativado, mas se você tem lido isso, percebe que não é tão simples. Os números que têm um sinal negativo como este são comumente chamados de assinado inteiros. Números como em um somador normal, onde o elogio de dois não é efetivado são chamados não assinado inteiros. Inteiros sem sinal podem ir para um valor mais alto, mas não podem ir abaixo de zero, enquanto inteiros com sinal podem ir apenas à metade, mas podem ir igualmente abaixo de zero. Isso significa que os dois números têm o mesmo intervalo, apenas em um local diferente, como este (isto é, com um número de 8 bits):
Sem sinal: 0-255 assinado -128-127
Deve-se observar que alguns efeitos estranhos podem ocorrer ao usar o valor com sinal mais baixo (neste caso -128), portanto, isso deve ser evitado.
Agora que temos uma maneira positiva de representar nossos números negativos, é muito trivial implementar isso em um somador. Atualmente, nosso somador resolve
A + B
Queremos resolver
A - B
or
A + (−B)
Portanto, se inserirmos o complemento de dois de B, nosso somador torna-se um subtrator. Isso é facilmente implementado usando o bit Carry-in do bit menos significativo (primeiro) como "+1" e, em seguida, tudo o que resta é inverter B.
Há uma coisa importante a se observar ao implementar isso. Como é possível obter um número de complemento de dois, ao subtrair o dígito mais significativo deve ser invertido. Geralmente, é a execução do último somador.
Tudo isso pode ser implementado em um somador como:

Um bit de controle é adicionado ao circuito de forma que, quando está ligado, a unidade subtrai e, quando está desligado, a unidade adiciona. Depois disso, adicione portas XOR entre o bit de controle e cada entrada B. Roteie a saída de cada XOR para a entrada B de cada somador. Finalmente, para tornar o complemento da unidade Dois compatível, uma porta XOR final deve ser adicionada entre o bit de controle e o carry out do bit mais significativo.
Esta é a maneira mais simples de implementar negativos e subtrações em uma CPU, pois isso adicionará graciosamente e armazenará bem nos registradores. Se isso for implementado em uma calculadora, simplesmente subtraia 1 da saída e, em seguida, inverta todas as saídas, exceto a mais significativa. O bit mais significativo estará ativado se o número for negativo.
Para fazer um subtrator, basta inverter uma das entradas binárias (o 1º ou 2º número). Se o número for negativo, a resposta sai invertida. Em computadores reais, o primeiro bit (também chamado de sinal) decide se o número é positivo ou negativo, se você incluí-lo (aplicando a mesma regra de inversão), você pode detectar se o número é negativo ou se é apenas um número grande .
Unidades lógicas
Em circuitos, pode ser útil ter uma unidade lógica que irá, com base na entrada, decidir qual saída será escolhida. Essa unidade pode então ser usada para circuitos mais complexos, como uma ALU.
Este é um exemplo de unidade lógica de 2 bits que terá quatro estados dependendo da entrada.

As saídas estão na linha superior, com ordem 11, 00, 01, 10 (ordem de entrada: primeiro primeiro, segundo inferior).
Este é outro exemplo de uma versão simplificada usando códigos de Gray. A saída aparece nas tochas no final das linhas superiores. Esse design pode ser estendido a qualquer número de bits, mas as limitações práticas devido a considerações de temporização restringem o uso de mais de um byte ou algo assim. As saídas são acionadas pelas entradas 11, 01, 00, 10, respectivamente.

Unidade lógica aritmética
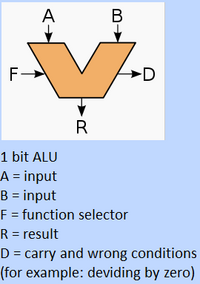

A unidade lógica aritmética (ALU) é a parte central da CPU. Ele faz cálculos e processamento lógico e, em seguida, passa essas informações para um registrador. A ALU, com base na entrada, seleciona uma função específica, a executa e, em seguida, fornece o resultado.
A ALU mostrada abaixo é uma ALU de 1 bit com as funções: ADD, AND, XOR. Leva as entradas A e B e, em seguida, executa as funções selecionadas. Leia sobre os somadores para ver como funciona a função ADD. XOR e AND são funções básicas explicadas na página de circuitos lógicos. Pode haver mais funções adicionadas a uma ALU, como multiplicação, divisão, OR, NAND ... etc. Essas funções podem, com algumas modificações, ser adicionadas a esta ALU de 1 bit.
Esta ALU de 1 bit pode ser vinculada entre si para criar uma ALU de tantos bits quanto possível. Assim como os somadores, você precisa conectar o Carry out (Cout) ao Carry in (Cin) da próxima ALU
Esquema ALU de 1 bit

Esta é uma captura de tela do ALU real de 1 bit no Minecraft. Você pode visualizar a ALU em 3D aqui.

Redstone
Veja em: Modelo: Redstone / conteúdo [editar || Tutoriais | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Introdutório |
| ||||||||||||
| Geral |
| ||||||||||||
| Desafios |
| ||||||||||||
| Construções |
| ||||||||||||
| Sustentável |
| ||||||||||||
| Encantador e fundido |
| ||||||||||||
| Blockbreaking |
| ||||||||||||
| Mecanismos |
| ||||||||||||
| servidores |
| ||||||||||||
| Técnico |
| ||||||||||||
| desatualizado |
| ||||||||||||