Este artículo necesita una limpieza para cumplir con la guía de estilo. [discutir] Por favor ayude a mejorar esta página. La página de discusión puede contener sugerencias.
Este artículo necesita una limpieza para cumplir con la guía de estilo. [discutir] Por favor ayude a mejorar esta página. La página de discusión puede contener sugerencias.
 Este artículo utiliza esquemas de MCRedstoneSim.
Estos deben convertirse para usar {{esquema}} si es posible.
Este artículo utiliza esquemas de MCRedstoneSim.
Estos deben convertirse para usar {{esquema}} si es posible.
Contenido
- 1 sumadores
- 1.1 Versión 1
- 1.2 Sumador en línea
- 1.3 Versión 2
- 1.4 Versión 3
- 1.5 Adición rápida
- 1.6 Sumadores de pistón
- 1.7 Sumador de 4 bits
- 1.8 Sumador alternativo de 4 bits
- 2 Restar
- 3 unidades lógicas
- 3.1 Unidad lógica aritmética
Sumadores
versión 1

Captura de pantalla del juego del sumador completo
Sumador completo 1
Ver en: Tutoriales / Puertas lógicas / Sumador completo 1 [editar] Sumador completoUn sumador completo toma dos entradas A y B y una entrada Carry y produce las salidas Sum y Carry. Se basa en dos puertas XOR, dos puertas AND y una puerta OR. Con un poco de pensamiento, estas puertas se pueden comprimir (ya que las puertas AND y XOR ya existen en el juego, y una puerta OR puede ser simplemente un cable de redstone).
A y B son las entradas de bit y C 'es el acarreo. Produce una suma en S y un acarreo en C. Cuando los módulos sumadores completos están en mosaico juntos, C' y C se conectarán, lo que permite que el acarreo se propague a el siguiente módulo.
Esquema de sumador completo
 Media víbora
Media víbora
El medio sumador es casi idéntico al sumador completo, excepto que se quita la segunda puerta XOR y la salida de la primera puerta XOR se convierte en S. No hay acarreo (C '), pero el circuito de ejecución (C) todavía está encendido parte superior de la primera puerta XOR y proporciona un acarreo al primer sumador completo. Algunas ALU no usarán un medio sumador para el primer bit, para admitir INCREMENT (permitir un arrastre en el primer bit).
Sumador en línea
Sumador completo

Captura de pantalla del juego de la suma completa de 2 anchos
Este sumador completo es similar al anterior, excepto por el hecho de que tiene dos anchos y las entradas están alineadas verticalmente. Este diseño es ideal para minimizar el espacio horizontal y se puede construir en línea con dos buses redstone, eliminando el espacio requerido para expandir un bus para alcanzar las entradas de un sumador completo más amplio.
Esquema del sumador completo
| Video tutorial (ver en YouTube) |
|---|
versión 2
Sumador completoPuertas: XNOR (2), IMPLIES, NOT, OR, Y
Tamaño: 6 × 12 × 5 (incluidos los espacios de E / S)
Este sumador tomará 2 bits y un bit transferido (en realidad C, en lugar de C, un valor que se encuentra en la piedra roja en la esquina inferior izquierda de la capa 1) y los sumará todos, produciendo un bit de suma (S) y un acarreo. (en realidad C en lugar de C).
Al usar las puertas de arriba; tenga en cuenta las entradas y salidas. Quizás se pregunte por qué se utilizan tantas señales invertidas en lugar de la señal normal.
Los sumadores que se muestran aquí usan compuertas XNOR en lugar de compuertas XOR porque son más compactas y, como resultado, implica que se deben usar compuertas en lugar de compuertas AND, que también resultan ser más compactas.
Por lo tanto, para el sumador más compacto, se deben usar señales inversas. Estos sumadores son demasiado complejos para descifrarlos fácilmente con 2 capas por cuadrado, por lo que cada capa se ha dibujado por separado para facilitar el proceso de construcción.
Esquema del sumador completo Media víbora
Media víbora
Puertas: XNOR, IMPLIES
Tamaño: 5 × 4 × 4
Este sumador tomará 2 bits y los sumará. El bit resultante será la salida de S (suma). Si ambos bits son 1, habrá un arrastre y C se convertirá en 1 (C se convertirá en 0). Este medio sumador se puede modificar para crear una salida C no invertida, pero esta configuración se utiliza para que pueda implementarse como el inicio de una cadena de sumadores completos.
Extensión: para aquellos que son nuevos en redstone avanzada como yo, es más fácil entenderlo así: digamos que la salida B (C) tiene una puerta NOT que invierte la señal y conduce a una puerta de hierro o una puerta de pistón, etc. La salida A (S) es conectado a pistones pegajosos que controlan el suelo. Digamos, en aras del argumento, que hay un bloque 1 × 1 × 1 NO afectado por los pistones pegajosos, este es el bloque de seguridad. Cuando active la entrada A, tanto la puerta se abrirá como el piso caerá, si está parado sobre el bloque de seguridad, entonces no caerá. La entrada B controlará solo el piso, pero si la entrada A está en la entrada B los controlará a ambos. Cuando ambos están activados, la entrada A solo afectará al piso. Esto significa que si está fuera del servidor y no quiere que nadie entre, deje A y B encendidos, cuando desactivan A, el piso se caerá, pero la puerta permanecerá cerrada, por lo que si conocen el secreto, aún no pueden entrar.
Esquema de la media víbora

versión 3
Sumador completoTamaño: 5 × 6 × 3
La entrada y la salida de transporte están alineadas para conectar fácilmente muchos de estos módulos en serie.
Esquema del sumador completo
Agregar rápidamente
Al construir circuitos digitales avanzados como computadoras y multiplicadores, los sumadores utilizados deben ser lo más rápidos posible para garantizar la máxima velocidad de ejecución. Los sumadores simples tienen un problema fundamental de velocidad que numerosos diseños de sumadores intentan corregir para acelerar. El problema es el retraso de propagación de acarreo: retraso causado por la forma en que los sumadores toman prestados los acarreos. Podemos ver esto cuando hacemos el problema 1111 + 0001:
1111 0001 ---- 1110
Este es el primer paso del proceso de adición, XORing de las dos entradas. Debido a que había dos unos en el bit menos significativo, la puerta AND se activa y se traslada al siguiente bit:
1 1111 0001 ---- 1100
Pero aquí está el problema: ahora necesita pedir prestado un carry nuevamente, porque, en el lugar de los dos, hay dos. Esto se hace mediante el AND de la salida del primer medio sumador con el acarreo del bit anterior y esto es un gran problema. Porque, durante el siguiente bit, usted Y el prestado llevan una y otra vez. Cada puerta AND toma 2 tics, por lo que, para calcular todos los acarreos que deben sumarse en el paso final, se necesitan 2 ticks por 4 bits, u 8 ticks.
Imagina que ves el problema 999 + 1. No te quedas sentado pensando "9 + 1 es 10, lleva 1, entonces 9 + 1 es 10, lleva el 1, entonces 9 + 1 es 10, entonces 1000". Es la misma situación en un circuito avanzado.
Los verdaderos ingenieros eléctricos y los redstoners creativos han diseñado circuitos que calculan los transportes sumadores más rápido que este método secuencial.
Por cierto, los sumadores que calculan los acarreos uno a la vez de esta manera se denominan Sumadores Ripple Carry.
Sumadores de pistón
Una de las formas más sencillas y clásicas de resolver el problema de la ondulación es usar compuertas Y instantáneas que usan pistones. Estos sumadores son simples y rápidos, pero son inconstantes porque usan pistones. Cuando los bloques se caen accidentalmente, todo el circuito se rompe. Los pistones también tienen problemas de sincronización que pueden ser terriblemente inconvenientes cuando se construye un circuito avanzado que depende en gran medida de la sincronización.

Siempre que se crea un acarreo, se envía a través del cable con la palanca puesta y, en lugar de pasar por una puerta Y, el pistón se retrae y el acarreo puede pasar al siguiente bit, lo que no agrega ningún retraso de propagación de acarreo ( hasta que se agote la intensidad de la señal).
Este video muestra una implementación sencilla de la lógica. El diseño es grande y extendido, por lo que es fácil ver cada parte individual del sumador y la lógica de acarreo.
Sumador de 4 bits
Puertas: XNOR (7), IMPLICA (4), NO (4), O (3) Y (3)
Tamaño: 23X12X5
¡Nota! El dígito menos significativo (dígito "unos") está a la izquierda del diagrama para que la progresión desde el medio sumador hasta los sumadores completos se pueda ver más claramente. Invierta el diagrama si desea una entrada convencional de izquierda a derecha.
Este sumador tomará números de 2, 4 bits (A y B) y los sumará, produciendo un bit de suma (S) para cada bit agregado y un acarreo (C) para la suma total. Los bits de suma están en el mismo orden que los bits de entrada, lo que en el diagrama significa que la salida S más a la izquierda es el dígito menos significativo de la respuesta. Este es solo un ejemplo de una cadena de sumadores; los sumadores se pueden encadenar de esta manera para sumar también números más grandes.
Esquema sumador de 4 bits
Sumador alternativo de 4 bits
La misma función pero un diseño diferente con 4 sumadores completos en lugar de 1 medio sumador y 3 sumadores completos
NOTA: los interruptores son las entradas A y B (entrada del interruptor superior C)
Esquema de sumador alternativo de 4 bits
Restando
Restar y sumar son lo mismo cuando se reduce a la idea de que, por ejemplo, 3-2 = 3 + (-2) = 1. Como ya tenemos el marco para sumar bits, es bastante sencillo restar por simplemente agregando el bit negativo. El problema radica en la representación de números negativos.
Todos estamos familiarizados con el concepto de la escuela primaria de "pedir prestado" en la resta de la siguiente columna de esta manera:
5623-128 -----
No somos capaces de sacar 8 de tres, por lo que "tomamos prestado" un 1 del siguiente decimal para permitirnos restar 8 de 13 en su lugar, lo que da como resultado 5
1 5623 - 128 ----- 5
Las computadoras no son capaces de hacer suposiciones, por lo que cuando una computadora necesita encontrar un negativo, no pone (ni puede) poner un signo negativo delante de la entrada. Simplemente resta de cero "préstamos" de la siguiente columna de la siguiente manera:
000000 - 3 ------- -999997
Esto es lo mismo en binario. Usemos, por ejemplo, un número binario de 4 bits para el ejemplo:
1 11 111 1111 0000 0000 0000 -0000 -0011 -0011 -0011 ----- ----- ----- ----- - 0011-1-01 -101
Podríamos repetir esto para siempre, pero sería inútil. Se trata de lo que hace un registro de 4 bits: se trunca después de 4 bits de datos. Entonces, después de truncar el número (lo que hice amablemente por usted en el ejemplo, de lo contrario, el número tendría un número infinito de unos a la izquierda). Gracias a esta pequeña ventaja, podemos hacer lo que queramos con los 1 después de los cuatro, incluido (que resultará fantásticamente útil más adelante) agregar un solo 0 delante de ellos.
10000 -0011 ----- 1101 <- NOTA: ¡Este número es positivo! ¡Éxito!
¿Recuerda cómo dijimos que nuestra redstone no tenía una forma especial de designar un negativo de un positivo? Acabamos de crear una forma. Si el (primer) bit más significativo de un número es 1, significa que es un número negativo. Esta fantástica ventaja de los números binarios es un teorema llamado "Complemento de dos".
Formalmente, el complemento a dos se define como:
El negativo de un número b con longitud de bits n es igual a 2n + 1 - b
Básicamente, lo que esto dice es que −b es solo la inversión de b (intercambia 1 por 0 y 0 por 1) más 1.
Lo que hemos hecho es convertir el primer bit en un "signo negativo" si está encendido, pero si has estado leyendo esto, te das cuenta de que no es tan simple. Los números que tienen un signo negativo como este se denominan comúnmente firmado enteros. Los números como en un sumador normal, donde el cumplido de dos no tiene efecto, se denominan no firmado enteros. Los enteros sin signo pueden ir a un valor más alto, pero no pueden ir por debajo de cero, mientras que los enteros con signo solo pueden llegar a la mitad, pero pueden llegar igualmente por debajo de cero. Esto significa que los dos números tienen el mismo rango, solo que está en una ubicación diferente como esa (esto es con un número de 8 bits):
Sin firmar: 0-255 Firmado -128-127
Cabe señalar que pueden producirse algunos efectos extraños cuando se utiliza el valor con el signo más bajo (en este caso -128), por lo que debe evitarse.
Ahora que tenemos una forma positiva de representar nuestros números negativos, es muy trivial implementar esto en un sumador. Actualmente nuestro sumador resuelve
A + B
Queremos que se resuelva
A - B
or
A + (−B)
Por lo tanto, si ingresamos el complemento a dos de B, nuestro sumador se convierte en un resta. Esto se implementa fácilmente utilizando el bit de arrastre del bit menos significativo (el primero) como "+1" y luego todo lo que queda es invertir B.
Hay una cosa importante a tener en cuenta al implementar esto. Debido a que es posible obtener un número en complemento a dos, al restar el dígito más significativo debe invertirse. Suele ser la ejecución del último sumador.
Todo esto se puede implementar en un sumador así:

Se agrega un bit de control al circuito de manera que cuando está encendido, la unidad resta, y cuando está apagado, la unidad suma. Después de esto, agregue puertas XOR entre el bit de control y cada entrada B. Dirija la salida de cada XOR a la entrada B de cada sumador. Finalmente, para hacer compatible el complemento Two de la unidad, se debe agregar una puerta XOR final entre el bit de control y la ejecución del bit más significativo.
Esta es la forma más sencilla de implementar negativos y restas en una CPU, ya que se sumará con elegancia y se almacenará bien en los registros. Si esto se va a implementar en una calculadora, simplemente reste 1 de la salida y luego invierta todas las salidas excepto la más significativa. El bit más significativo estará activado si el número es negativo.
Para hacer un resta, simplemente invierta una de las entradas binarias (el primer o segundo número). Si el número es negativo, la respuesta sale invertida. En computadoras reales, el primer bit (también llamado signo) decide si el número es positivo o negativo, si lo incluyes (aplicando la misma regla de inversión) puedes detectar si el número es negativo o si es solo un número grande .
Unidades lógicas
En los circuitos, puede resultar útil tener una unidad lógica que, en función de la entrada, decida qué salida se va a elegir. Una unidad de este tipo se puede utilizar para circuitos más complejos, como una ALU.
Este es un ejemplo de una unidad lógica de 2 bits que tendrá cuatro estados según la entrada.

Las salidas están en la fila superior, con el orden 11, 00, 01, 10 (orden de entrada: primero primero, segundo inferior).
Este es otro ejemplo de una versión simplificada que utiliza códigos Gray. La salida aparece en las antorchas al final de las filas superiores. Este diseño puede extenderse a cualquier número de bits, pero las limitaciones prácticas debidas a consideraciones de tiempo restringen el uso de más de un byte aproximadamente. Las salidas se activan mediante las entradas 11, 01, 00, 10, respectivamente.

Unidad aritmética lógica
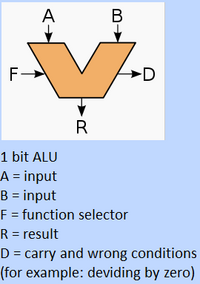

La unidad lógica aritmética (ALU) es la parte central de la CPU. Realiza cálculos y procesamiento lógico y luego pasa esta información a un registro. La ALU, basándose en la entrada, selecciona una función específica, la realiza y luego da el resultado.
La ALU que se muestra a continuación es una ALU de 1 bit con las funciones: ADD, AND, XOR. Toma las entradas A y B y luego realiza las funciones seleccionadas. Lea sobre los sumadores para ver cómo funciona la función AGREGAR. XOR y AND son funciones básicas que se explican en la página de circuitos lógicos. Se pueden agregar más funciones a una ALU, como multiplicación, división, OR, NAND ... etc. Estas funciones podrían, con algunas modificaciones, agregarse a esta ALU de 1 bit.
Esta ALU de 1 bit se puede vincular entre sí para crear una ALU de tantos bits como sea posible. Al igual que los sumadores, debe conectar el Carry out (Cout) al Carry in (Cin) de la siguiente ALU
Esquema de ALU de 1 bit

Esta es una captura de pantalla de la ALU de 1 bit real en Minecraft. Puede ver la ALU en 3D aquí.

Redstone
Ver en: Plantilla: Redstone / contenido [editar]| Tutoriales | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Introductorio |
| ||||||||||||
| General |
| ||||||||||||
| Desafíos |
| ||||||||||||
| Construcciones |
| ||||||||||||
| Sostenible |
| ||||||||||||
| Encantador y fundición |
| ||||||||||||
| Rompiendo bloques |
| ||||||||||||
| Mecanismos |
| ||||||||||||
| Servidores |
| ||||||||||||
| Apoyo técnico |
| ||||||||||||
| Anticuado |
| ||||||||||||